9x^4-9x^2+2=0 решить биквадратное уравнение

Подставим u=x² в уравнение. Это упростит применение формулы корней квадратного уравнения.

9u² − 9u + 2=0

Разлагаем на множители путем группирования.

9u² − 3u − 6u + 2 = 0

Вынесем наибольший общий делитель из каждой группы.

3u( 3u−1)−2(3u−1)=0

Разобьем полином на множители, вынося наибольший общий делитель, 3u−1

(3u−1)(3u−2)=0

Если любой отдельный множитель в левой части уравнения равен 0 , то и все выражение будет равняться 0

3u−1=0

3u−2=0

Приравняем 3u−1 к 0, затем решим относительно u

u = 1/3

Приравняем 3u−2 к 0, затем решим относительно u

u = 2/3

Итоговым решением являются все значения, обращающие (3u−1)(3u−2)=0 в верное тождеств

u = 1/3, 2/3

Произведем обратную замену u=x² в решенном уравнении

x² = 1/3

x² = 2/3

Решим первое уравнение относительно x

x = √3/3,−√3/3

Решим второе уравнение относительно x

x = √6/3,−√6/3

Результат можно выразить в различном виде.

Точная форма:

x = √3/3,−√3/3,√6/3,−√6/3
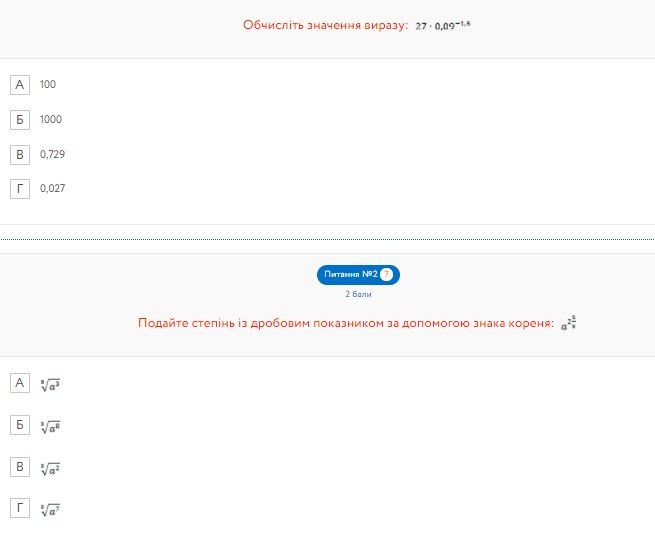
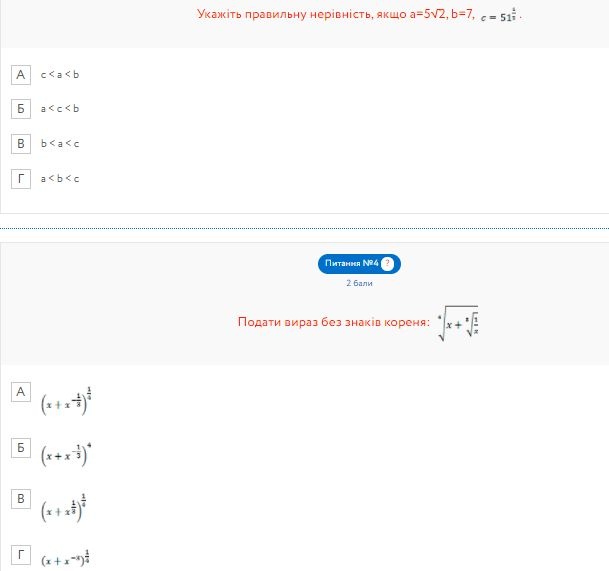
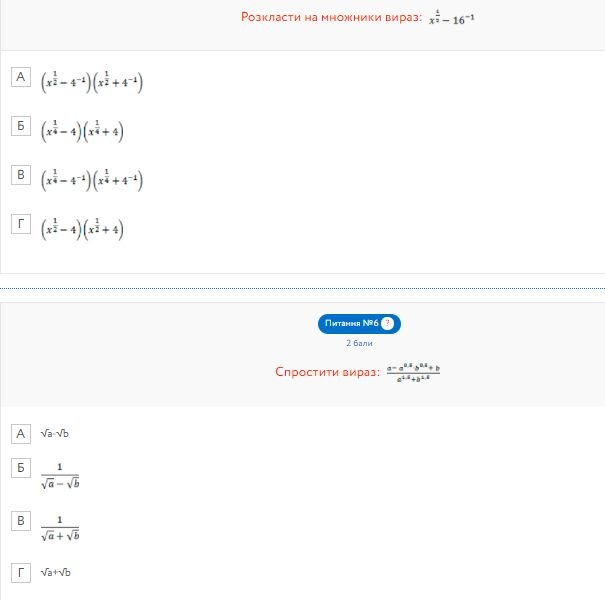
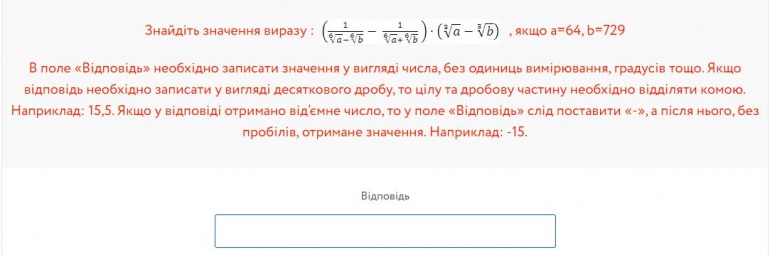