2. Упростите выражение ((a² - b²)/(a - b)) - ((a³ - b³)/(a² - b²))
3. Решите уравнение 5ᵡ+² * √5 = 1/25
4. Решите неравенство log₃(x + 1) > - 2
5. Найти cos(a), если sin(a) = 0,8 и π/2 < а < π
6. Решите уравнение √(x + 3) = x + 3
7. Найдите точки экстремума функции у = x³ - 6x² + 4
8. Для функции f(x) = cos2x найдите первообразную, график которой проходит через точку A(π/2;0)
9. Вершина С треугольника ABC соединена отрезком с точкой E, принадлежащей стороне AB так, что ∠ABC = ∠ACE
Найдите длину отрезка AE, если AB = 34 см, AC = 20 см
10. Сторона основания правильной треугольной пирамиды равна 6 см, а боковое ребро 5 см. Найдите площадь полной поверхности пирамиды.




Ответы:
2. Ответ: ab/(b + a)
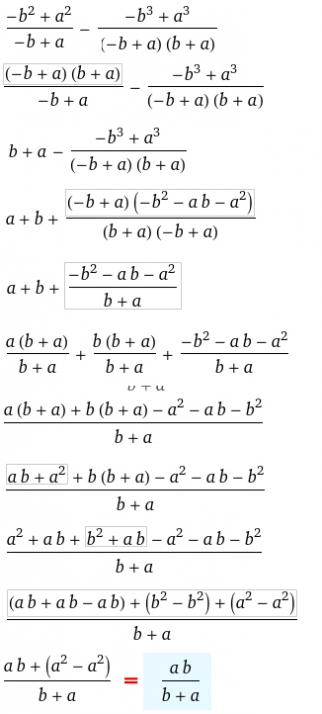
3. Ответ: x = -4,5
4. Ответ: (-8,9;∞)
5. cos(a) = -√(1 - 0,64 ) = -√0,36 = -0,6
Ответ: cos(a) = -0,6
6. Ответ: x = -2 и x = -3
7. (0,4) является максимумом функции у = x³ - 6x² + 4
(4,−28) является минимумом функции у = x³ - 6x² + 4
8. Ответ: F(x) = (1/2)*sin(2x) + C,
F'(x) = ((1/2)*sin(2x) + C) = (1/2)*cos(2x)*(2x) + C = cos(2x)
0=F(π/2) = (1/2)*sin(π) + С = (1/2)*0 + C = 0
C = 0 Искомая первообразная это F(x) = (1/2)*sin(2x)
10. S= √p(p-a)(p-b)(p-c)
p = (6 + 5 + 5)/2 = 8
S=√8(8-6)(8-5)(8-5)=√8 * 2 * 3 * 3 = 12 см²
S = 3 * 12 = 36 см²
S = S1+S3=36+9√3=51,59 см²
1
Отв. дан
Savage


9. △ABC ~ △ACE так как :
∠BAC - общий
∠ABC = ∠ECA по условию
треугольники подобны
составим пропорцию
AC/AE = AB/AC
AE = AC²/AB
AE = 20²/34 = 400/34 = 200/17 = 11(13/17) ≈ 11,7 см
1
Отв. дан
Savage


Для написания вопросов и ответов необходимо зарегистрироваться на сайте
Другие вопросы в разделе - Математика

Zuhn 838
2021-05-26 06:55:26

Leonardo
2021-05-21 11:32:26

Zuhn 838
2021-05-10 01:02:10

Amirkhan
2021-04-23 05:14:53