Даны вершины треугольника ABC. Найти: а) уравнение стороны AB; б) уравнение высоты CH; в) уравнение медианы AM; г) точку персечения медианы AM и высоты CH; д) уравнение прямой, проходящей через вершину C параллельно стороне AB; е) расстояние от точки C до прямой AB.Решение и чертёж. Огромное спасибо!!!!!!!!!!
A(–2,4) B(3,1) C(10,7)
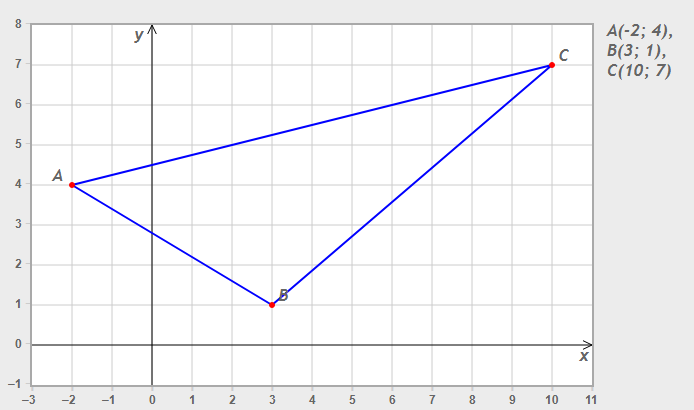
а) уравнение стороны AB;
Координаты векторов находим по формуле:
X = xj - xi; Y = yj - yi
здесь X,Y координаты вектора; xi, yi - координаты точки Аi; xj, yj - координаты точки Аj
Положим A(xA;yA) = A(−2;4), B(xB;yB) = B(3;1), C(xC;yC) = C(10;7)
Длина стороны: |AB| = √(3 - (-2)²) + (1 - 4)² = √5² + (-3)² = √25 + 9 = √34
Уравнение стороны: AB: (x - xA)/(xB - xA) = (y - yA)/(yB - yA) ⇔ (x - (-2))/(3 - (-2)) = (y - 4)/(1 - 4) ⇔ (x + 2)/5 = (y - 4)/(-3) ⇔ 3x + 5y - 14 = 0
б) уравнение высоты CH;
Уравнение стороны: CH: (x - 10)/(1 - 4) = (y - 7)/(-2 - 3) ⇔ (x - 10)/(-3) = (y - 7)/(-5) ⇔ 5x - 3y - 29 = 0
в) уравнение медианы AM
Уравнение стороны AM: (x - (-2))/(6,5 - (-2)) = (y - 4)/(4 - 4) ⇔ (x + 2)/8,5 = (y - 4)/0 ⇔ y - 4 = 0
д) уравнение прямой, проходящей через вершину C параллельно стороне AB
C ∥ AB: (x - 10)/(3 - (-2)) = (y - 7)/(1 - 4) ⇔ (x - 10)/5 = (y - 7)/-3 ⇔ 3x + 5y - 65=0
е) расстояние от точки C до прямой AB
Найдем длину BC
Длина стороны: |BC| = √(10 - 3)²) + (7 - 1)² = √7² + 6² = √49 + 36 = √85

Другие вопросы в разделе - Геометрия

1.Точка D належить відрізку AB, причому BD:BA=1:4. Через точку ...



 ...
... ...
...