2. Раскройте скобки (x/4 +0,3y)²
(x/4)² + 2*x/4*0,3y + (0,3y)²
x²/16 + 0,3x/2y + 0,09/y²
3. Найдите логарифм по основанию а числа, представленного в виде
степени с основанием а: 12³ =1728
Логарифм 1728 по основанию 12 равен 3
log₁₂1728 = 3
4. Вычислить: log₂32
Логарифм 32 по основанию 2 равен 5
logₒ(x) = y эквивалентно bᵒ = x
2^x=32
2^x=2⁵
Так как основания одинаковые, выражения равны только тогда, когда равны степени.
x=5
5. Определите четность или нечетность функции:
у = 8 + 5sin x
Функция четная. График функции симметричен относительно оси ординат.
6. Найдите область определения:
у = 5 + sin2x
Областью определения выражения являются все вещественные числа, кроме тех, при которых выражение не определено. В данном случае нет вещественных чисел, при которых выражение было бы неопределенным.
Запись в виде интервала:
(−∞,∞)
Нотация построения множества:
x|x∈R}
Область определения:
(−∞,∞),[x|x∈R]
7. Решить уравнение:
sinx - 1/2 = 0
x = arcsin(1/2)
arcsin(1/2) = Пи/6
x = Пи/6
Функция синуса принимает положительные значения в первом и втором квадрантах. Для определения второго решения вычитаем решение из Пи, чтобы найти решение во втором квадранте.
x= Пи - Пи/6
x = 5Пи/6
Период функции sin(x) равен 2Пи, то есть значения будут повторяться через каждые 2Пи радиан в обоих направлениях
x =Пи/6 + 2Пиn, 5Пи/6 + 2Пиn для всех целых n
x₁ = Пи/6
x₂ = 5Пи/6
8. Решить дробно-рациональное уравнение
(3o² - 5o - 8)/(o² - 1) = 0
(3o² +3o - 8o - 8)/(o² - 1) = 0
3o(o + 1) - 8(o - 1)/(o² - 1) = 0
((o + 1)(3o - 8))/((o + 1)(o - 1)) = 0
(3o - 8)/(o - 1) = 0
3o - 8 = 0
o = 8/3
9. Решить систему неравенств
3x +3 ≤ 2x + 1
3x - 2 ≤ 4x + 2
Решим
3x + 3 ≤ 2x + 1 относительно x
x ≤ −2
Решим 3x−2≤4x+2 относительно x
x≥−4
Найдем пересечение x≤−2 и x≥−4
−4≤x≤−2
Запись в виде интервала:
[−4,−2]
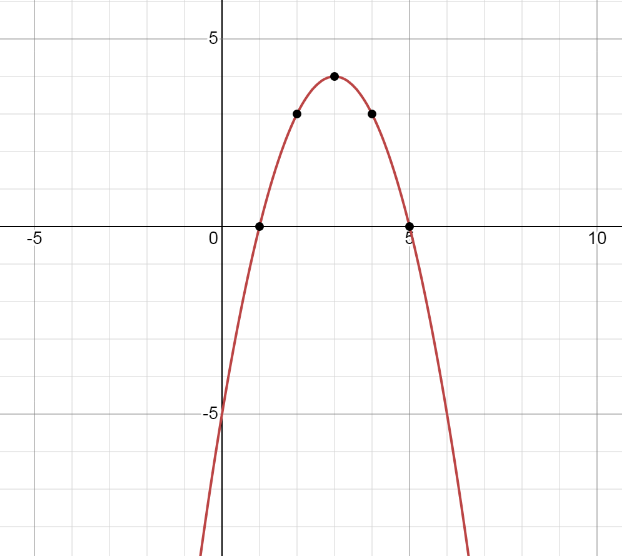
10. Построить график функции
у = -x² + 6x - 5
и укажите наибольшее значение этой функции
Используя уравнение в виде y=a(x−h)²+k, определим значения a, h и k
Вершина: (3,4)
Ось симметрии: x=3
Направляющая: y=17/4
f(max) x=ax²+bx+c встречается в x=−b²
x = -b/2a
x = -6/2*(-1)
x = 3
Вычисляем f(3) = 4
максимум (3,4)
11. У Пети есть 7 монет по 1 рублю и 3 монеты по 2 рубля. Петя случайным образом выбирает 1 монету номиналом 1 рубль и 1 монету номиналом 2 рубля. Сколькими способами он может это сделать?
C¹₇ = 7!/(1!(7 - 1)!) = 7!/6! = 7
C¹₃ = 3!(1!(3 - 1)!) = 3
7 * 3 = 21

Другие вопросы в разделе - Математика

Определите концентрацию раствора, массой 500 г, содержащего 50 г ...



 ...
... ...
...