
Пожалуйста, мне надо решить первый
вариант
1. Решить систему уравнения методом Краммера и Гусса.
x - 2y + z = -2
3x + y - 2z = 3
2x - y + 3z = 3
∆ = 1*1*3 + (-2)*(-2)*2 + 1*3*(-1) - 1*1*2 - 1*(-2)*(-1) - (-2)*3*3 = 3 + 8 - 3 - 2 - 2 + 18 = 22
∆₁ = (-2)*1*3 + (-2)*(-2)*3 + 1*3*(-1) - 1*1*3 - (-2)*(-2)*(-1) - (-2)*3*3 = -6 + 12 - 3 - 3 + 4 + 18 = 22
∆₂ = 1*3*3 + (-2)*(-2)*2 + 1*3*3 - 1*3*2 - 1*(-2)*3 - (-2)*3*3 = 9 + 8 + 9 - 6 + 6 + 18 = 44
∆₃ = 1*1*3 + (-2)*3*2 + (-2)*3*(-1) - (-2)*1*2 - 1*3*(-1) - (-2)*3*3 = 3 - 12 + 6 + 4 + 3 + 18 = 22
x = ∆₁/∆ = 22/22 = 1
y = ∆₂/∆ = 44/22 = 2
z = ∆₃/∆ = 22/22 = 1
2. Даны вершины пирамиды ABCD
A (1,2,1)
B (5,0,3)
C (2,-3,-4)
D (3,1,-2)
∠BAC = arccos((24+51−67)/(2*2√6*51)) = arccos(1/51 * √34) ≈ 83.435°
S(ABC) = 1/2 √20² - 22² - 18² = √302

V = 12
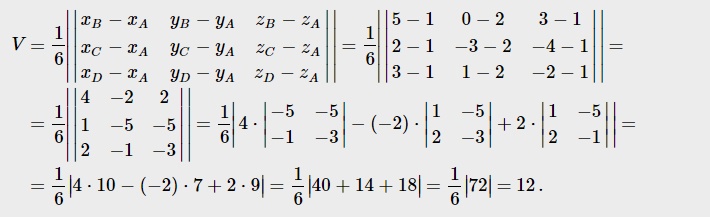
Высота:
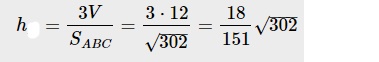
3. Даны вершины треугольника ABC
A (2,1)
B (-1,4)
C (-2;-3)
Уравнение медианы из вершины A:
Обозначим середину стороны BC буквой М. Тогда координаты точки M найдем по формулам деления отрезка пополам
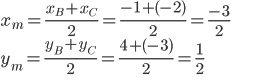
Уравнение медианы AM найдем, используя формулу для уравнения прямой, проходящей через две заданные точки. Медиана AМ проходит через точки A(2;1) и М(-3/2;1/2), поэтому:
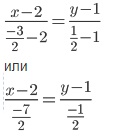
Уровнение высоты:
Прямая, проходящая через точку N0(x0;y0) и перпендикулярная прямой Ax + By + C = 0 имеет направляющий вектор (A;B) и, значит, представляется уравнениями:
(x - x₀)/A = (y - y₀)/B
Найдем уравнение высоты через вершину A
(x - 2)/-7 = (y - 1)/1

4x² + y² - 4x + 2y - 6 = 0
определить тип кривой
Исходное уравнение определяет эллипс (λ1 > 0; λ2 > 0)
Центр - C(1/2; -1)

Другие вопросы в разделе - Математика


Найдите наибольшее и наименьшее значения функции f(x) = −x^3− ...



 ...
... помогите решить контрольную ...
помогите решить контрольную ...